Zurück
zum
LDfM, zur Fachgruppe
Mathematik,
zur Fakultät
für
Mathematik, Informatik und Naturwissenschaften, zur RWTH.
Grundlagen der Geometrie
Protokoll vom 16.11.00 (FM)
Zurück zum
13.11.00; zur Übungsstunde vom
15.11.00;
weiter zur Stunde vom
20.11.00.
Ziel der Vorlesung war es, die Gültigkeit des großen Satzes
von Pappus in einem konkreten Beispiel für einen projektiven
Raum zu überprüfen.
Gegeben sei ein Links-Vektorraum V über einem Schiefkörper
K mit dim (V) ³ 3.
Dann sei P(V):= (P, G,
I), wobei P die Menge aller eindimensionalen Teilräume von
V bezeichnet. Sie werden von jeweils einem Element x
¹
0
aus V erzeugt.
G bezeichnet die Menge aller zweidimensionalen Teilräume
von V. Sie werden von linear unabhängigen Paaren (u,
v) mit Elementen u und v aus V erzeugt. X
I g wird gelesen als: X ist Teilraum von g.
Damit ist P(V) ein projektiver Raum im Sinne der Axiome.
Ein projektiver Raum erfüllt den großen Satz von Pappus,
wenn gilt:
Sind g, h zwei sich schneidende Geraden mit Schnittpunkt
S und A, B, C von S verschiedene Punkte auf g
sowie A', B', C' von S verschiedene Punkte auf h, so
liegen die Schnittpunkte (die nach dem projektiven Veblen-Young-Axiom existieren)
der Geradenpaare (AB', A'B), (BC', B'C) und (AC', A'C)
auf einer Geraden.
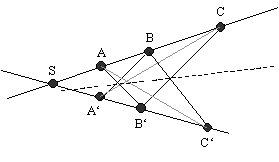
Um die Gültigkeit überprüfen zu können, müssen
wir zunächst alle vorkommenden Punkte und Geraden als Elemente von
P(V) darstellen (siehe oben).
Wir erhalten als Darstellung für die Punkte die Erzeugnisse S
= <s>, A = <a>, B = <b>, C
= <c>, A' = <a'>, B' = <b'>
und C' = <c'>.
Für die Gerade g erhalten wir g = SA = <s,
a>, wobei das Paar (s, a) linear unabhängig in V
ist, da S und A zwei verschiedene Punkte sind. Analog stellen
wir die Gerade h = SA' als Erzeugnis <s, a'> dar.
(s, a, a') ist linear unabhängig, da g und h
zwei verschiedene Geraden sind, und ist damit Basis für W:=
<s, a, a'>. Alle weiteren Punkte können wir in dieser Basis
darstellen.
Der Punkt B liegt auf der Geraden g, was in unserer Struktur
bedeutet, daß das Erzeugnis <b> Teilraum von <s,
a> ist. Wir können also b als Linearkombination von s
und a darstellen: b = ls
+ ma. Ohne Beschränkung der Allgemeinheit
seien beide Koeffizienen ungleich Null, ansonsten wäre B = A
und die Schnittpunkte lägen auf der Geraden AC', also der Satz
erfüllt.
Da wir b und a noch nicht definiert haben, können
wir sie durch 1/l b beziehungsweise m/l
a ersetzen und erhalten die Gleichung
b = s + a,
haben damit also beide Koeffizienten eliminiert.
Analog verfahren wir bei der Darstellung der anderen Punkte und erhalten
für sie die Gleichungen
| c |
= |
s + |
ga, |
|
| b' |
= |
s + |
|
ba', |
| c' |
= |
s + |
|
a'. |
Für die Schnittpunkte der Geraden definieren wir die Bezeichnungen
| X |
:= |
AB' Ù A'B, |
| Y |
:= |
BC' Ù B'C, |
| Z |
:= |
AC' Ù A'C. |
Der Punkt X, in unserer Struktur das Erzeugnis <x>, läßt
sich also darstellen durch
<x> = X = <a, b'> Ù
<a', b>,
also durch Linearkombinationen aus a und b' beziehungsweise
a' und b.
Mit Anwenden der Eindeutigkeit der Basisdarstellung und Ersetzen von
bisher nicht definierten Größen (siehe oben) lösen wir
das Gleichungssystem der beiden Darstellungen für x zu
x = a + s + ba'.
Analog verfahren wir bei der Darstellung der anderen Schnittpunkte und
erhalten die Gleichungen
| y |
= |
tga + |
ss
+ ts + |
sba', |
| z |
= |
ga + |
s + |
a'. |
Sollte der große Satz von Pappus in unserer Struktur erfüllt
sein, die Punkte X, Y und Z also auf einer Geraden
liegen, so müßte (x, y, z) linear abhängig in
V sein.
Durch Auflösen des Gleichungssystems für x, y
und z gelangen wir zu folgender Bedingung für die lineare Abhängigkeit
in V:
(s-1t)
* (g - 1) = (g
- 1) * (s-1t).
Der große Satz von Pappus gilt also in P(V) genau
dann, wenn K kommutativ ist.
Zurück zum
13.11.00; zur Übungsstunde vom
15.11.00;
weiter zur Stunde vom
20.11.00.
Zurück zum
Seitenanfang,
zu
Grundlagen
der Geometrie,
zur Hauptseite,
zum LDfM, zur Fachgruppe
Mathematik,
zur Fakultät
für
Mathematik, Informatik und Naturwissenschaften, zur RWTH.

